- Полный обзор Sony Ericsson Xperia mini: миниатюрность не в ущерб функциональности Bluetooth - это стандарт безопасного беспроводного переноса данных между различными устройствами разного типа на небо
- Смартфоны для девушек Samsung La Fleur: цены на Galaxy Ace La Fleur, Duos, s3 и mini На самсунге la fleur
- Обзор форумных CMS Изобилии board powered by smf
- Помощь: Просмотр темы Проверены profile powered by smf
- Понятие операторных скобок
- Чем отличается выделенный сервер от хостинга для игровых серверов?
- Скачивание драйверов для ноутбука Lenovo G570 Комплект полезных программ для ноутбука Lenovo IdeaPad G570
- Драйверы для ноутбука Lenovo G570
- Апл айфон 7 32 гб серебристый
- Лучшие калькуляторы для iPhone и iPad
- Восстановление пароля Webmoney Не могу восстановить свой аккаунт в webmoney
- Грамотная раскрутка аккаунта в Periscope Программа для накрутки просмотров в перископе
- Клавиша Option на Mac: особенности и описание Клавиша shift на клавиатуре mac
- Как разлочить iphone 4 от 4s
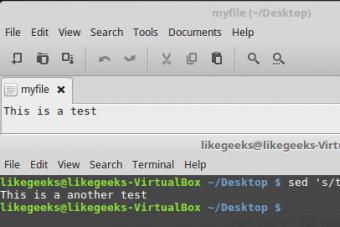
- Sed — Ай да Linux Wiki Опции программы sed
- Лучшие дистрибутивы Linux для новичка
- Как установить игру новый человек паук на компьютер
- Главные особенности в игре
- Как установить (изменить) браузер используемый по умолчанию и сделать в нем Гугл или Яндекс умолчательным поиском Как перейти на поисковую систему гугл
- Что включает в себя роботс
- Ошибка подключения или неверный код MMI
- Samsung Galaxy J2 Prime: бюджетный смартфон с неплохой камерой Плюсы и минусы Samsung Galaxy J2 Duos J200
- Сталкер золотой шар завершение скачать торрент
- Идеальные настройки для сталкер зов припяти
- Почему залипает курсор мыши?
- DX11 и DX12: а есть ли между ними разница?
- Восстанавливаем карты памяти и флешки SanDisk
- Восстановление флешки: определение контроллера, прошивка флешки
- Как разработчики портят статистику игрокам
- Не запускается игра World of Tanks
- Электронная почта сервисы рейтинг
- Для чего нужны и какие бывают
- Как зарегистрировать и зайти в электронный дневник школьника через госуслуги Зарегистрироваться электронный дневник школьника вход
- Как в госуслугах зарегистрировать и зайти в электронный дневник школьника
- Накрутка комментариев на youtube – Ваш канал будет популярен Лайки в вк микс
- Vkmix — бесплатная раскрутка Вконтакте, Instagram, YouTube
- Как восстановить (сбросить) забытый пароль к Apple ID для iCloud, iTunes и App Store
- Почему iTunes не видит iPhone: причины, устранение проблемы
- Как удалить все driver pack solution?
- Три способа включения тачпада
Sed — Ай да Linux Wiki Опции программы sed
В прошлый раз мы говорили о функциях в bash-скриптах, в частности, о том, как вызывать их из командной строки. Наша сегодняшняя тема...